Интерпретация квантовой механики
Дан краткий обзор основных представлений (интерпретаций) квантовой механики. Каждая из рассмотренных интерпретаций содержит ряд спорных положений, обсуждение которых позволяет выработать свое понимание механизма парадоксальных квантовых явлений. Статья адресована студентам-экономистам, изучающим концепции современного естествознания, и всем читателям, интересующимся вопросами: «Какая реальность стоит за гранью квантово-механического эксперимента?» или: «Действительно ли наше восприятие в некотором смысле формирует физический мир?» Автор полагает, что развитие квантовых информационных технологий невозможно без ответа на эти фундаментальные вопросы.
Ключевые слова: квантовая механика, проблема измерения, волновая функция, нелокальность, запутанные состояния, квантовая томография. Введение.
Введение.Надо ли интерпретировать квантовую механику? Многие скажут, что не надо. Например, Л. Д. Ландау очень не одобрял такие занятия. Но если признать эту установку правильной, то можно свести физику до уровня поварского дела: соблюдай «рецепты», решай задачи и не занимайся ерундой! Однако, решение прикладных задач — важный, но не единственный аспект квантовой механики. Не менее, а, может быть, и более важно понять глубинный смысл парадоксальных квантовых явлений. Без этого понимания нельзя представить себе прогресс квантовой информатики, начинающей практически осваивать новые технологии. Но и это еще не все. Ведь поразительные открытия последних лет говорят о том, что мы находимся на пороге смены физической картины мира и постижения тайны человеческого сознания. Понимая это, многие светлые умы занимались и занимаются разработкой интерпретаций квантовой механики. Автор насчитал 17 таких интерпретаций, достойных упоминания. Каждая из них содержит зерно истины. Критическому обзору этих представлений и посвящена настоящая статья.
1. Копенгагенская интерпретация. Это наиболее известная, или, как говорят, ортодоксальная трактовка квантовой механики, которой придерживается большинство физиков [1–3]. Сформулирована Н. Бором и после 5-го Сольвеевского конгресса (1927) стала общепринятой и остается таковой вплоть до сегодняшнего дня. Была развита в работах В. Гейзенберга, М. Борна, В. Паули, А. М. Дирака, К. фон Вайцзеккера, В. А. Фока. Уточнялась учениками Бора. Существует несколько вариантов копенгагенской интерпретации, отличающихся трактовкой некоторых положений (интерпретация Гейзенберга-Фока, Уилера, фон Неймана, Пригожина и др.).
Согласно копенгагенской трактовке, состояние микрообъекта задается некоторой комплексной функцией Ψ (x, y, z, t) координат и времени (волновая функция или Ψ-функция). Основное уравнение квантовой механики — уравнение Шредингера. В общепринятых обозначениях:
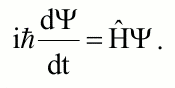
Сама волновая функция, фигурирующая в уравнении Шредингера, не имеет физического смысла, а квадрат модуля её интерпретируется как плотность вероятности обнаружить микрообъект в данном месте пространства. Фаза волновой функции не интерпретируется вообще. Ранний Бор считал, что статистика возникает из-за неконтролируемого воздействия прибора на объект. В дальнейшем было показано, что воздействие прибора тут ни при чем, а статистика носит более принципиальный характер. При измерении происходит коллапс (редукция) волновой функции (термин введен фон Нейманом и Дираком в 1932 г.): Ψ-функция мгновенно обращается в нуль всюду, кроме того места, где обнаружена частица. Таким образом, в копенгагенской интерпретации система перестает быть смешением состояний и выбирает одно из них в тот момент, когда происходит наблюдение. Измерение рассматривается как взаимодействие макроскопического (классического) прибора и наблюдателя с микрообъектом. Реальными признаются только результаты измерений: спрашивать о сущности явления до измерения запрещается. Например, не имеет смысла вопрос, что представляет собой электрон до наблюдения его в эксперименте. Квантовомеханические предсказания относятся только к результатам наблюдения. Реальность окружающего мира не отрицается, но указывается на принципиальную ограниченность анализа взаимодействия между микрообъектом и прибором (« феноменологическая реальность»). Объяснение квантово-механического явления состоит не в раскрытии его «механизма», а в построении непротиворечивой теории. В копенгагенской интерпретации можно отметить два принципиально важных положения:
– не существует никакой реальности вне наблюдения;
– реальность «создаётся» наблюдателем.
Копенгагенская интерпретация предполагает для объяснения квантовых явлений наличие классических объектов (прибора, наблюдателя) и рассматривает редукцию волновой функции как результат взаимодействия квантовой системы с классической. А так как любой классический объект на микроскопическом уровне квантовый, то возникает замкнутый круг. Если же признать, что все объекты квантовые, то понятие измерения теряет обычный смысл и заменяется понятием квантовой корреляции.
2. Интерпретация Гейзенберга-Фока. Следующая трактовка, которую мы рассмотрим, предложена Гейзенбергом и развита советским академиком В. А. Фоком [4, 5]. Как уже отмечалось, копенгагенская трактовка, разделяемая в принципе большинством физиков того времени, утверждает, что не нужно искать более глубокого описания и понимания реальности, данной нам в эксперименте. Только феномены являются реально существующими, и помимо них нет никакой более глубокой реальности. Гейзенберг был одним из немногих физиков, пытающихся понять и описать «квантовую реальность». По Гейзенбергу, за квантовым феноменом действительно нет никакой реальности, но в совершенно ином смысле, чем вкладывал в это утверждение Бор. За квантовым феноменом, считает Гейзенберг, находится только «полуреальность», не мир фактически существующего, а всего лишь потенция, «тенденция» к осуществлению.
Гейзенберг утверждал, что квантовая механика возвращает нас к идее множественности бытия, аристотелевским понятиям «бытие в возможности» и «бытие в действительности». Гейзенберг не развил достаточно последовательно такую трактовку, и фактически это было сделано Фоком. Фок вводит понятие «потенциальных возможностей» и «осуществившегося» в результате измерения, практически полностью согласуясь в этом с Гейзенбергом.
Точку зрения Гейзенберга и Фока разделяет большое число физиков и философов, в частности, К. Поппер, выдвинувший концепцию предрасположенности («propensity») к реализации сингулярного события. По Попперу, волновая функция описывает не известные из классической физики свойства микрообъектов, а потенции (предрасположенности) объектов проявлять те или иные свойства. Квантовая реальность — это реальность потенций поведения микрообъектов. Физически реальными являются вероятности. Понятие «продрасположенность», по Попперу, отсылает нас к «ненаблюдаемым диспозиционным свойствам физического мира, ... наблюдению же доступны только некоторые наиболее внешние проявления этой реальности» (цитир. по [1]). Предрасположенности, согласно Попперу, являются физическими реалиями подобно силам в механике. Индетерминизм и интерпретация вероятности как предрасположенности означают переход к новой физической картине мира, в которой вероятностные законы имеют более высокий статус, чем динамические законы классической механики.
3. Интерпретация Уилера. Развитием копенгагенской трактовки квантовой механики является интерпретация, предложенная учеником Бора Дж. Уилером [1, 2]. Эта трактовка акцентирует внимание на втором положении копенгагенской интерпретации. Бытие Вселенной по Уилеру есть результат «акта участия наблюдателя» в процессе самоосуществления Вселенной, «ввергающей себя в бытие посредством актов участия». Термин «наблюдатель» можно заменить, по мнению Уиллера, термином «участник». Редукции волновой функции происходит в определенный момент процесса измерения, при этом реализуется одна из возможностей поведения микрообъекта. Прибор и «наблюдатель» регистрируют этот факт редукции и тем самым доводят физический процесс до полноты, явленности. Без редукции на завершающей стадии эксперимента не имеет смысла говорить о существовании физических явлений. «Вид» реальности конституируется самим актом установления факта редукции волновой функции к фактически полученному результату. Акт редукции регистрируется наблюдателем. По словам Уилера, «наблюдатель столь же существенен для проявления Вселенной, как и Вселенная для проявления наблюдателя».
4. Интерпретация фон Неймана. В интерпретации, тесно связанной с теорией измерения Дж. фон Неймана, утверждается, что непосредственно само сознание наблюдателя, связанное с измерительной аппаратурой, и создаёт реальность [1, 7]. «Мы всегда должны делить мир на две части — наблюдаемую систему и наблюдателя. То, что такую границу можно поместить сколь угодно далеко внутрь организма действительного наблюдателя, и составляет содержание принципа психофизического параллелизма», — писал фон Нейман. К сторонникам включения «феномена сознания» в основания квантовой механики относятся Е. Вигнер, Р. Пенроуз, а в России — проф. М. Б. Менский. Последний вообще ставит знак равенства между понятиями «выбор альтернативы» и «осознавание». Сознание рассматривается как мост между естествознанием и гуманитарным знанием, между материализмом и идеализмом. Фон Нейман является также основоположником квантовологической трактовки квантовой механики (см. далее п. 7).
5. Интерпретация Пригожина. Другое название — брюссельская интерпретация. В качестве следующей интерпретации квантовой механики рассмотрим трактовку И. Р. Пригожина, призывающего отказаться от классического понятия «галилеевского объекта» [1, 8]. Пригожин, предлагает исключить из квантовой механики «субъективный элемент, связанный с наблюдателем». Парадокс, по мнению Пригожина, состоит в том, что обратимое уравнение Шредингера может быть проверено лишь с помощью необратимых измерений, которые это уравнение, по определению, не может описывать. Отсюда он делает вывод, что квантовая механика не может быть замкнутой теорией. По Пригожину, фундаментальную роль в современной физике (и не только в квантовой механике) играет понятие «стрела времени» и, следовательно, необратимые процессы. Они «имеют преимущество» перед процессами обратимыми, а последние — есть всего лишь частный случай, т. е. «классическое исключение» из общего правила. В квантовой механике акт измерения есть как раз необратимый процесс, элемент необратимости, вмешивающийся в систему. Об этом же читаем у Ландау и Лифшица: «...процесс измерения в квантовой механике имеет двуликий характер — его роли по отношению к прошлому и будущему не совпадают. По отношению к прошлому оно верифицирует вероятности различных возможных результатов, предсказываемыми по состоянию, созданному предыдущим измерением. По отношению же к будущему оно создаёт новое состояние. В самой природе процесса заложена, таким образом, глубокая необратимость. Эта необратимость имеет важное принципиальное значение. ... Основные уравнения квантовой механики сами по себе обладают симметрией по отношению к изменению знака времени; в этом отношении квантовая механика не отличается от классической. Необратимость же процесса измерения вносит в квантовые явления физическую неэквивалентность обоих направлений времени, т. е. приводит к появлению различия между будущим и прошедшим» [9]. Обсуждая интерпретацию Пригожина, можно отметить следующее. Процессы, протекающие в реальном мире, в самом деле необратимы во времени, а законы классической механики и основное уравнение квантовой механики — уравнение Шредингера — обратимы. Но уравнение Шредингера не есть уравнение движения. Из его обратимости не вытекает непосредственно обратимость движений.
6. Многомировая интерпретация. Предложена Хью Эвереттом (США, 1957) [1, 10]. Проф. М. Б. Менский называет эту интерпретацию «самой интересной и самой радикальной». Предположим, что производится измерение координаты частицы, находящейся в состоянии суперпозиции. В результате получается с некоторой вероятностью одно из возможных значений этой величины. Согласно копенгагенской трактовке, волновая функция коллапсирует, т. е. мгновенно обращается в нуль всюду, кроме точки, в которой обнаружена частица. По Эверетту же утверждается, что коллапс волновой функции вообще не происходит никогда. Любое квантово-механическое измерение «расщепляет» Вселенную на реально существующие макроскопические копии. В каждой из них реализуются те или иные возможности, содержащиеся в исходной суперпозиции. Каждый компонент квантовой суперпозиции представляет собой отдельную и равноправную физическую реальность. Вселенная расщепляется на ряд вселенных-ветвей, каждая из которых соответствует своему возможному исходу события. То, что мы воспринимали как коллапс, означает, что наше сознание выбрало определенный путь через эти ветви, и поэтому наблюдается один набор результатов вместо другого, из миллиардов возможностей. Другие копии нашего сознания могут наблюдать другие возможные исходы в других вселенных-ветвях. В практическом плане данная концепция совпадает с копенгагенской.
При рассмотрении идеи Эверетта надо иметь в виду, что слово «существование» может употребляться в двух смыслах. Объект может существовать во времени и пространстве. Например, мы говорим: существует Земля или существует электромагнитное поле и т. д. Но возможно существование в чисто логическом смысле. Это предполагается, когда говорится о существовании, например, целых чисел, электромагнитной теории, самого пространства и времени или миров Эверетта.
Классические альтернативы воспринимаются сознанием отдельно друг от друга. М. Б. Менский предложил расширенную многомировую концепцию, согласно которой разделение альтернатив отождествляется с явлением сознания. Это объясняет классический характер альтернатив и необычные проявления сознания, возникающие «на краю сознания» (то есть в режиме сна или транса), когда становится возможным её доступ к другой альтернативе классической реальности. Квантовая эволюция в данной концепции обратима, поэтому все моменты времени в квантовом мире эквивалентны. Впечатление от течения времени возникает лишь в сознании.
В настоящее время многомировая интерпретация активно обсуждается в связи с космологическими проблемами. «Многомировая интерпретация представляет собой естественный выбор для квантовой космологии, которая описывает вектор состояния для Вселенной в целом. Нет ничего более макроскопичного, нежели Вселенная. Она может априори не иметь классических подсистем. В ней может не быть "внешнего" наблюдателя » (В. Зурек). Среди сторонников её много известных ученых. Допускают многомирие Дж. Уилер, Р. Фейнман, Е. Вигнер, Д. Дойч, С. Хокинг, М. Тегмарк, А. Шимони, в России — проф. М. Б. Менский и многие другие.
7. Квантовологическая интерпретация. Фон Нейиан показал, что все парадоксы квантовой механики могут быть разрешены на основе неклассической (квантовой) логики [11]. Первую систему многозначной логики — трёхзначную логику высказываний — разработал польский логик Я. Лукасевич (1920). Наше познание основано на двузначной аристотелевской (булевой) логике, где предполагается, что высказывания могут быть только истинными и ложными. У Аристотеля справедлив закон исключения третьего, а именно при оценке суждения может быть дан один из двух возможных ответов: « истинно» оно или «ложно». Например, это такие суждения, как «электрон находится в точке с координатами x, y, z» или «импульс частицы равен p»; Лукасевич, а применительно к квантовой механике фон Нейман, добавляют к ним «может быть» или «не определено». В трёхзначной (небулевой) логике квантово-механические парадоксы не возникают.
Логику можно сравнить с геометрией: и геометрия, и логика не априорны. Геометрия соответствует переходу от ньютоновской механики к релятивистской (от геометрии Евклида к геометрии Римана), и точно так же логика — переходу от классической механики к квантовой (от логики Аристотеля к логике Лукасевича–Неймана).
Квантовая трёхзначная логика применима и к событиям казалось бы далеким от квантовой механики. Например, подбросим монету вверх. Монета определенно подчиняется аристотелевской логике «либо–либо». Она упадёт на пол либо орлом вверх, либо решкой вверх. Но пока монета кувыркается в воздухе, она находится в состоянии «может быть». Еще пример: издали мы можем принять человека за своего знакомого. И пока не подойдем к нему ближе и не проверим это предположение, человек этот находится в состоянии « может быть». Духом аристотелевской логики проникнут вердикт присяжных «виновен — не виновен». Традиционное следование аристотелевской логике в масштабах страны и мира часто приводит к трагическим последствиям. Сюда относится догматически-однозначная оценка роли личности в истории, деление людей на красных и белых, оценка экономических успехов той или иной политической системы и т. д. «Люди игнорируют квантовое "может быть", потому что большинство никогда не слышало о квантовой логике или трансакционной психологии (трансакционная психология — наука о том, как мозг обрабатывает полученные данные, психология восприятия, А. В.), но еще и потому, что традиционные политические идеологии и религии на протяжении тысячелетий учили людей — и продолжают учить сегодня — действовать с нетерпимостью и преждевременной уверенностью», — писал по этому поводу Р. А. Уилсон [12].
Сторонники этой трактовки — Дж. Биркхоф, Дж. фон Нейман, Д. Финкельштейн и др.
8. Неореалистическая интерпретация (Теория скрытых параметров). Сторонники этой трактовки, среди которых были А. Эйнштейн, Л. де Бройль, Д. Бом (после 1951 года) и др., верят в возможность построения более глубокой теории, позволяющей объяснять квантовые явления, но базирующейся на обычных классических представлениях [1]. Парадоксальные результаты квантовых измерений объясняются неполнотой наших знаний о микромире. В неореалистических трактовках предполагается, что как макромир, так и микромир, состоят из обычных классических объектов, свойства которых не зависят от наблюдения. Математический аппарат квантовой теории является, таким образом, лишь удобным феноменологическим аппаратом, правильно описывающим эксперименты. Здесь можно упомянуть теорию волны-пилота Луи де Бройля и теорию квантового потенциала Бома, различные теории со скрытыми параметрами. В теории де Бройля, например, квантовая частица «ведется» определенной волной-пилотом, подчиняющейся уравнению Шредингера. «Квантовый потенциал» Бома, управляет движением частицы посредством так называемой «активной (или действующей) информации» обо всем окружении данной частицы, т. е. о Вселенной в целом. Квантовый потенциал не зависит от расстояния и, таким образом, обеспечивает прямую взаимосвязь между квантовыми системами. Таким образом Дэвид Бом и Луи де Бройль пытались свести квантовую теорию к классической детерминистической теории. После известных опытов по проверке неравенств Белла и экспериментов с «отложенным выбором» стала понятной бесплодность таких попыток.
9. Холистская интерпретация. Предложена в 80-х гг. прошлого века Д. Бомом [1, 13]. По этой трактовке Универсум подобен особой голограмме. Весь мир отражается во всех своих частях, подобно тому, как кусочек голограммы содержит всю информацию обо всей целой голограмме. Бом говорит о том, что в отдельных частях структуры как бы «свернуты», «завернуты», и потом могут быть, соответственно, извлечены. «Имплицитный порядок» задан повсюду. «Составными элементами» этого являются не классические «галилейдекартовские» объекты, a действие, движение, или, как их называет сам Бом — «holomovents» или некоторые целостные «голономные» движения.
«Внутренний порядок», холистический момент являются для Бома отличительными признаками квантовой механики. ЭПР-пара демонстрирует «неразложимость» мира, его нелокальный характер. По Бому существует «невидимая система регулирования всего сущего». Бом утверждает, что мы должны отказаться от картезианского дуализма, картезианского понимания объекта и перейти к холистической, целостной трактовке. Идеи Бома разделяет швейцарский нейрофизиолог Карл Прибрам. Если соединить теории Бома и Прибрама, мы получим радикально новый взгляд на мир: наш мозг математически конструирует объективную реальность путём обработки частот, пришедших из другого измерения — более глубокого порядка существования, находящегося вне пространства и времени. Мозг — это голограмма, свернутая в голографической вселенной.
Другим вариантом такой интерпретации квантовой механики является точка зрения швейцарского физика Ганса Примаса. Его основная идея состоит в том, что мы должны отказаться от разделения мира на единые объекты или события. Сам мир для Примаса является целостным, неделимым и единственным объектом.
Универсум, с позиций холизма, не является скоплением одиночных, друг с другом взаимодействующих, но существующих самих по себе объектов, поскольку эти объекты существуют только в связи с их отношением к наблюдателю и его абстракциям.
10. Ансамблевая интерпретация. Под ансамблевыми интерпретациями будем понимать интерпретации, выдвигающие на первый план понятие статистического коллектива (ансамбля) [1, 5, 14]. Ярким сторонником такой концепции был в СССР профессор Д. И. Блохинцев. Копенгагенская (ортодоксальная) интерпретация, как известно, трактует квантовую механику как теорию, описывающую в своих основаниях поведение одной физической системы (электрона, атома и т. д.). Понятие статистического коллектива появляется при этой интерпретации как логически производное: оно формулируется при инструментальной (эмпирической) интерпретации математического аппарата квантовой теории. Кроме того, понятие статистического коллектива возникает в квантовой статистической механике, распространяющей принципы квантовой механики на системы, состоящие из многих частиц. При ансамблевой же интерпретации сама суть квантовой механики связывается с понятием статистического коллектива.
В своих работах Блохинцев подчеркивает статистический характер квантовых ансамблей, отмечает отличие этой статистики от классической, указывает на объективный (не зависящий от наблюдателя) характер квантовых ансамблей и управляющих ими закономерностей. Наблюдателю отводится более скоромная роль. По Блохинцеву, квантовая механика неприменима к отдельным микрообъектам, так как никакой микрообъект нельзя изучать вне его окружения. Однако знание объективной реальности могло быть «в принципе» достигнуто путём изучения больших количеств микрочастиц. Центральным здесь является понятие квантового ансамбля. По мнению Блохинцева, вероятность, содержащаяся в волновой функции, происходит из серии повторяющихся измерений. Таким образом, когда говорят о волновой функции одной частицы или одной системы, то на самом деле речь идёт о большом количестве таких частиц или систем. Совокупность таких частиц, являющихся независимыми друг от друга и имеющих возможность выступать в роли материала для последовательных независимых экспериментов, и была названа ансамблем.
Позицию Блохинцева критиковал Фок. Он отмечает фундаментальные положения квантовой механики, использованные Блохинцевым: а) ансамбль есть набор частиц, которые независимо друг от друга находятся в том же состоянии, характеризуемом волновой функцией; в) состояние частицы следует понимать только как принадлежность частицы к определенному ансамблю, так что с) волновая функция не относится к отдельной частице. Фок показывает, что эти положения противоречат друг другу: «В утверждении (а) содержится определение состояния отдельной частицы через её волновую функцию, в утверждении же (с) отрицается, что волновая функция относится к отдельной частице. Далее, в утверждении (а) ансамбль определяется через волновую функцию, а в утверждении (в) волновая функция определяется через ансамбль. Это есть порочный круг» (цитир. по [5]).
11. Интерпретация Фейнмана. Данная формулировка квантовой механики предложена Ричардом Фейнманом 1942 году [15]. Вместо метода Гамильтона здесь используется метод Лагранжа (берется интеграл вдоль траектории от функции Лагранжа по времени). Позднее метод Фейнмана получил название «квантование путём континуального интегрирования». В основе фейнмановской интерпретации находится не уравнение Шредингера для волновой функции, а бесконечномерное интегрирование по всем возможным траекториям. Впервые интеграл по траекториям встречается в работах Эйнштейна и Смолуховского по теории броуновского движения. Вероятность прохождения броуновской частицы по некоторой траектории пропорциональна (мера Винера [16]) eS/ћ , где S — действие, т. е. интеграл по времени от лагранжиана; ћ — постоянная Планка. Фейнман рассматривает не только классические траектории, но все мыслимые траектории, соединяющие точки, между которыми происходит переход. Все траектории вносят вклад, одинаковый по абсолютной величине, а фаза каждого вклада представляет собой классическое действие, выраженное в единицах ћ. В классическом приближении S >> ћ , и оказывается наиболее важной лишь одна траектория. Такой подход позволяет наглядно связать квантовое и классическое описание движения. Фейнман показал, что интеграл по траекториям можно свести к дифференциальному уравнению Шредингера. Таким образом, данная формулировка математически эквивалентна копенгагенской. Первичной у Фейнмана все-таки остается волновая функция, поэтому по существу его трактовка сводится к перезаписи уравнения Шредингера. Развитием этого подхода является интерпретация Г. В. Рязанова, рассмотревшего также движение вспять по времени и отрицательные вероятности, что позволило дать представление квантовой механики без волновой функции (см. далее).
12. Транзакционная интерпретация. Предложил Джон Крамер (1986). В основе данной интерпретации лежит представление о том, что квантовый переход частицы, состоящий из излучения и поглощения, может рассматриваться как одиночная транзакция между источником и детектором частицы (термин заимствован из информатики: в информатике транзакция — это совокупность операций над данными, которая, с точки зрения обработки данных, либо выполняется полностью, либо совсем не выполняется). Волновая функция интерпретируется как реальная волна, физически существующая в пространстве. Как известно, волновое уравнение электромагнитной волны и любой другой волны, содержащей вторую производную по времени, допускает решение, соответствующее запаздывающей и опережающей волне [24]. Опережающие волны распространяются в обратном направлении во времени и обычно игнорируются как не имеющие физического смысла. Транзакция же сформирована обеими волнами: запаздывающей волной-предложением, распространяющейся от источника из настоящего в будущее, и опережающей волной-подтверждением, распространяющейся от детектора из будущего в настоящее (см. диаграмму в [17]). Фазовые соотношения этих двух волн таковы, что в сумме волны дают до излучения и после поглощения нулевое поле излучения (деструктивная интерференция). Природа допускает различные транзакции с вероятностями, соответствующими стандартной квантовой теории, но в каждом случае реализуется только одна транзакция. Авторы [18] считают, что «следует фокусироваться на переходе как таковом (транзакции), а не на излучении и поглощении по отдельности; надо рассматривать квантовый переход (транзакцию) как единичное физическое событие». В такой «редакции» прослеживается попытка ввести пространство элементарных событий. Движение «против времени» вводится также в темпоральной и рязановской интерпретации (см. ниже).
13. Информационная интерпретация. Предложил Войцех Зурек (США, 2001) [19]. Согласно этому подходу, состояние системы изменяется (суперпозиция переходит в смесь) вследствие обмена информацией между системой и окружением. Классическая реальность возникает из квантовой, если объём этой информации достаточен для того, чтобы различить компоненты суперпозиции. Роль «наблюдателей» при этом могут играть не только люди, но и любые объекты окружения. В этой связи можно упомянуть поразительный опыт, поставленный в Венском университете несколько лет тому назад А. Цайлингером и сотрудниками. Речь идёт об известном эксперименте с двумя щелями: зависимости от способа наблюдения на экране получается либо интерференционная картина (если неизвестно, через какую щель проходит частица) или частицы ведут себя классически (если каким-то образом проконтролировать прохождение частиц через щели). С помощью лазера осуществлялся «внутренний нагрев» молекулы фуллерена C70 (фуллерен — аллотропная форма углерода, молекула феллерена — выпуклый замкнутый многогранник), т. е. изменялась энергия колебаний атомов углерода. При низкой температуре наблюдалась интерференционная картина, т. е. молекулы обнаруживали волновые свойства. При повышении температуры картина становилась все менее контрастной, а при температуре около 3000 К исчезала совсем, и молекулы вели себя как классические частицы. Это объясняется тем, что при повышении температуры молекулы получают все большую энергию, частота излучения соответственно повышается (длина волы уменьшается). В конце концов излучение становится таким коротковолновым, что можно в принципе определить, через какую щель прошла молекула. Декогеренция происходила, хотя не было никакого детектора и наблюдателя. Роль «наблюдателя» играла окружающая среда. Это значит, что для перехода суперпозиции в смесь существенно не наличие наблюдателя, как такового, а наличие информации о том, через какую щель прошла молекула.
14. Модальная интерпретация. Модальными в логике называются суждения, в которых дается характеристика связи между субъектом и предикатом (высказыванием) или выражается отношение к ней автора суждения. Модальную интерпретацию квантовой механики предложил американский философ Б. ван Фраассен (1973), провозгласивший так называемый «конструктивный эмпиризм» — принцип, согласно которому «научная деятельность является скорее конструированием, чем открытием: конструированием моделей, которые должны быть адекватны явлению, а не открытием истины, имеющей отношение к ненаблюдаемому» (цитир. по [20]). Цель науки по Фраассену — дать эмпирически адекватные теории. Модальная интерпретация не предполагает чего-либо нового относительно квантовых состояний. Она лишь подчеркивает тот факт, что эти состояния определяют лишь вероятностные диспозиции значений динамических переменных. Согласно модальной интерпретации кроме обычного квантового состояния, представляемого волновой функцией, вводится динамическое состояние, которое определяется через значения динамических переменных, характеризующих данную систему. Квантовая механика рассматривается как теория, приписывающая определенные значения этим динамическим переменным. Динамические переменные имеют определенное значение, даже если физическая система не находится в собственном состоянии соответствующего оператора (т. е. независимо от того, проводится ли измерение этих переменных или нет). Динамические переменные, таким образом, дают более тонкое описание состояния системы.
Это означает, что динамические состояния, вводимые при модальной интерпретации, не полностью определены квантовыми состояниями и не выводятся из них. Вместе с тем квантовые состояния, изменяющиеся в соответствии с уравнением Шредингера, накладывают статистические связи на изменения динамических состояний. «Состояние системы описывает то, что может случиться со значениями физических величин, — пишет о квантовом состоянии ван Фраассен, — то же, что реально происходит с ними, лишь возможно по отношению к состоянию физической системы и не может быть дедуцировано из этого состояния» (цитир. по [20]).
15. Интерпретация Рязанова. Предложена Г. В. Рязановым в (1958) [21, 22]. Позволяет получить квантово-механическое описание, основываясь только на образах и понятиях классической статистики. Волновая функция для такой формулировки не нужна и может быть сохранена только для проведения вычислений. Как и в интерпретации Фейнмана, здесь в качестве пространства элементарных событий рассматривается множество траекторий перемещения частицы их положения 1 в положение 2. Наряду с фейнмановскими траекториями рассматриваются также траектории, соответствующие движению вспять по времени. Траектории могут иметь петли, на отдельных участках которых частица движется назад по времени. Квантовые траектории описываются непрерывными и нигде не дифференцируемыми функциями (такие функции можно изучать, используя дробные размерности и свойства фрактальных множеств). Таким образом, пространство элементарных событий у Рязанова расширяется по сравнению с пространством фейнмановских траекторий. Вместо меры Винера, вводится знакопеременная мера Рязанова: вероятность прохождения по данной траектории полагается пропорциональной cos( S / ћ) . Это означает, что вероятность прохождения частицы по траектории может быть как положительной, так и отрицательной. Введение отрицательных вероятностей можно сравнить с введением отрицательных чисел. При суммировании траекторий все петли взаимно уничтожаются («теорема об интерференции траекторий») и остается группа траекторий 1 → 2 («вперед») и 2 → 1 («назад»). Вероятность перехода 1 → 2 выражается интегралом
P(1 → 2) = ∫ P(1 → 3)P(3 → 2)Dx(t) ,где 3 — произвольная промежуточная точка, а интеграл берется по всем траекториям, соединяющим точки 1 и 2. Замечательным в интерпретации Рязанова является то, что первичным понятием здесь является вероятность элементарного события — перехода частицы из состояния 1 в состояние 2, а не волновая функция, без которой вообще можно обойтись. Основным уравнением также является уравнение для вероятности. Можно показать (и это делается в [21]), что из этого уравнения вытекает уравнение Шредингера и формулировка квантовой механики с использованием понятия волновой функции Ψ. Этим интерпретация Рязанова принципиально отличается от всех прочих интерпретаций, включая интерпретацию Фейнмана. Принцип Рязанова содержит в себе всю квантовую механику: волновую функцию, принцип суперпозиции, операторы и коммутационные соотношения. 16. Темпоральная интерпретация. Предложена С. И. Кузнецовым [23] (2007). В основе данной концепции лежит представление Уилера и Фейнмана (1942) об опережающих (движущихся против времени) и запаздывающих (движущихся по времени) электромагнитных волнах [24]. Взаимодействующие заряженные частицы излучают противоположно направленные волны — опережающую и запаздывающую. Опережающая электромагнитная волна переизлучается на зарядах, встречающихся на её пути. При каждом таком переизлучении также возникает две волны: одна — опережающая, которая продолжает углубляться в прошлое, и другая запаздывающая, возвращается к текущему моменту времени. Все переизлученные запаздывающие волны одновременно приходят в тот самый момент, когда произошел акт излучения, складываются и гасят ту опережающую волну, которая их породила. Остается только одна волна — запаздывающая, распространяющаяся из настоящего в будущее. Мы не можем уловить волну из будущего, — она мгновенно гасится в момент излучения. Опережающие волны из будущего оказываются ненаблюдаемы. Остаются «правильные» запаздывающие волны, уходящие в будущее и несущие информацию о прошлом.
Применительно к квантовой механике дело обстоит так. Рассмотрим пару ЭПР-частиц. Сигнал, испущенный одной из коррелирующих частиц («темпоральная волна »), распространяется вдоль её мировой линии против течения времени и достигает точки рождения ЭПР-пары, отражается от нее и возвращается из прошлого в настоящее, двигаясь вдоль мировых линий обеих частиц этой пары. То же самое происходит и с сигналом, испущенным второй частицей. Возвращаясь из прошлого в виде двух отраженных темпоральных волн, этот сигнал достигает текущего положения не только второй, но и первой частицы. Новое квантовое состояние каждой из частиц является результатом интерференции двух вернувшихся из прошлого темпоральных волн: собственной волны и волны, посланной частицей-партнером. Обмен сигналами приводит к согласованию состояний частиц в соответствии с законами сохранения суммарных значений их физических параметров. В представлении Кузнецова нет будущего времени, а есть только настоящее и прошлое, не застывшее, но активно влияющее на настоящее. По мнению автора, такой подход решает проблему нелокальности: частицы ЭПР-пары обмениваются информацией мгновенно, хотя скорость распространения темпоральной волны равна скорости света.
17. Томографическая интерпретация. Авторы называют эту интерпретацию квантовой механики вероятностной [25, 26]. Попытки сформулировать квантовую теорию наиболее близким образом к формулировке классической теории, предпринимались с самого появления квантовой механики. В 1932 году Е. Вигнер ввел функцию, являющуюся аналогом функции распределения в фазовом пространстве для классической частицы. В 1949 году Дж. Мойал получил уравнение эволюции функции Вигнера, похожее на классическое уравнение, но содержащее постоянную Планка и всю информацию, эквивалентную информации, содержащейся в матрице плотности. Однако, и функция Вигнера, и уравнение Мойала содержали отрицательные вероятности, не имеющие, по мнению авторов, данной интерпретации, физического смысла. Напомним, что в интерпретации Рязанова (см. выше) рассматриваются и положительные, и отрицательные вероятности.
Квантовая томография использует для описания квантовых состояний неотрицательные функции распределения вероятностей — симплектические томограммы. Недавно было доказано, что в рамках схемы симплектической томографии, обобщившей схему оптической томографии, можно описать квантовое состояние, используя измеримую положительную вероятность (работы проф. В. И. Манько и его итальянских коллег). Дана формулировка квантовой механики, в которой квантовые состояния описываются распределениями вероятностей, как в классической статистической механике для систем с непрерывными переменными (координата и импульс), а также и для систем с дискретными переменными (спины, двухуровневые атомы, кубиты и кудиты). В квантовой механике традиционно использовалась одна система отчёта в фазовом пространстве. Здесь же рассматриваются различные системы отсчёта в фазовом пространстве, как в специальной теории относительности рассматриваются различные системы отсчёта, связанные преобразованиями Лоренца. В квантовой задаче дополнительные параметры, соответствующие разным системы отсчёта, заменяют информацию, закодированную в фазе волновой функции (напомним, что в копенгагенской трактовке фаза волновой функции не интерпретируется никак).
Рассмотрение ансамбля систем отсчёта позволяет свести стандартный формализм квантовой механики к стандартному формализму классической статистической механики. Таким образом, в некотором смысле томографическая интерпретация квантовой механики оказывается подобна рязановской.
Подведем итог. Все рассмотренные выше интерпретации можно разделить на две категории: признающие и не признающие исходным понятием волновую функцию. В последнем случае введение волновой функции рассматривается как вычислительный прием. Ряд интерпретаций повторяют исходные представления Бора, лишь оттеняя некоторые моменты. «Крупномасштабно» можно выделить копенгагенскую, многомировую и рязановскую интерпретации. Первая из них носит позитивистский характер, как бы это ни отрицали Бор и его ученики. Вторая — разрешает проблему коллапса волновой функции. И, наконец, трактовка Рязанова позволяет объяснить квантовые явления в рамках классической статистики ценой введения отрицательных вероятностей и движения вспять по времени.
Литература1. Севальников А. Современное физическое познание: в поисках новой онтологии. М. : Изд-во ИФ РАН, 2003. 144 с.
2. Севальников А. Ю. Возвращение метафизики. URL: http://www.intelros.ru/pdf/orientyri/5/04.pdf.
3. Севальников А. Ю. К истории интерпретаций квантовой механики в России, или от физики к метафизике. URL: http://www.chronos.msu.ru/RREPORTS/osnovaniya_fiziki/sevalnikov_interpretatsii.pdf.
4. Фок В. А. Об интерпретации квантовой механики // Философские проблемы современного естествознания. М., 1959.
5. Грэхэм Л. Естествознание, философия и науки о человеческом поведении в Советском Союзе, гл. 10 (Квантовая механика). URL: http://scepsis.ru/library/id_1165.html.
6. Поппер К. Квантовая механика и раскол в физике. М. : Логос, 1998. URL: http://www.libbooks.ru/bookbox_99187.html.
7. Нейман фон Дж. Математические основы квантовой механики. М. : Наука, 1964. 366 с. URL: http://top-lib.ru/561546-dzh-fon-neyman-matematicheskie.html.
8. Пригожин И. Р. Конец определенности. Время, хаос и новые законы Природы. М. ; Ижевск : НИЦ «Регулярная и хаотическая динамика», 2000. 208 с. Режим доступа: URL: http://www.klex.ru/5c6.
9. Ландау Л. Д., Лифшиц Е. М. Квантовая механика, нерелятивистская теория. М. : Наука, 1974. С. 41.
10. Менский М. Б. Концепция сознания в контексте квантовой механики // УФН. Т. 175. No 4. 2005. URL: www.chronos.msu.ru/RREPORTS/mensky_kontseptsia.pdf.
11. Багров В. Г. Открытие неклассической логики поведения квантовых объектов — одно из удивительных достижений современной физики // Соросовский образовательный журнал. 2000. No 7. С. 72–78. URL: http://www.zntu.edu.ua/base/i3/rpf/k2/pogosov-lect/0007_072.pdf.pdf.
12. Уилсон Р. А. Квантовая психология / Перевод с англ. под ред. Я. Невструева. К. : ЯНУС, 1998. 224 с. URL: http://brb.silverage.ru/zhslovo/psiho/raw/?r=kp или: http://www.gumer.info/bibliotek_Buks/Psihol/Wils/index.php.
13. Талбот Майкл. Голографическая Вселенная. 2004. URL: http://lib.rus.ec/b/126854.
14. Печенкин А. А. Ансамблевые интерпретации квантовой механики в США и СССР // Вестник Московского университета. Серия 7. Философия. No 6. 2004. С. 103–121. URL: http://www.scorcher.ru/art/theory/quants_entanglement/entanglement4.php.
15. Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям. М. : Мир, 1968. 383 с.
16. Винер Н. Нелинейные задачи в теории случайных процессов. М. : ИЛ. 1961. 159 с.
17. Cramer John G. The Transactional Interpretation of Quantum Mechanics // Reviews of Modern Physics. 1986. Juli. Vol. 58. P. 647–688. Русский перевод: Крамер Дж. Транзакционная интерпретация квантовой механики. URL: http://ru.laser.ru/transaction/tiqm/index.html.
18. Куракин П. В., Малинецкий Г. Г. (Институт прикладной математики им. М. В. Келдыша). Как пчелы могут объяснить квантовые парадоксы. URL: http://quantum3000.narod.ru/my_papers/intro.html.
19. Zurek W. H. Decoherence and the Transition from Quantum to Classical. URL: http://xxx.lanl.gov/abs/quant-ph/0306072.
20. Зурек В. Декогеренция и переход от квантового мира к классическому // Los Alamos Science. No 27. 2002. URL: http://www.chronos.msu.ru/RREPORTS/zurek_dekogerencia.pdf.
21. Печенкин А. А. Модальная интерпретация квантовой механики как «антиколлапсовская» интерпретация // Философия науки. Вып. 6. М. : ИФ РАН, 2000. C. 31–38. URL: http://iph.ras.ru/page49880192.htm.
22. Рязанов Г. В. Квантовомеханические вероятности как суммы по путям // ЖЭТФ. 1958. Т. 35. Вып. 1. С. 121–131.
23. Кухаренко Ю. А. Рождение стрелы времени из квантового хаоса // Наука и технология в России. 1997. No 3 (20). URL: http://anomalia.kulichki.ru/text6/385.htm.
24. Кузнецов С. И. Темпоральная интерпретация квантовой механики // Пространство и время: физическое, психологическое, мифологическое: сборник трудов V Международной конференции. М. : Культурный центр «Новый Акрополь», 2007. С. 33–42. URL: http://www.chronos.msu.ru/RREPORTS/kuznetsovsi_interpretatsiya.htm.
25. Фейнман Р. КЭД — странная теория света и вещества. М. : Наука, 1988. 143 с.
26. Манько В. И. Обычная квантовая механика без волновой функции // УНЦ «Фундаментальная оптика и спектроскопия». Сборник лекций. Выпуск 1. Москва, 1998.
27. Манько О. В. Томографическое представление квантовой механики и квантование на основе звездочного произведения // Теоретическая физика. Т. 9. 2008. С. 101–113. URL: http://theorphys.samsu.ru/pdf/9/th_09_09_Manko.pdf.